Difference between revisions of "Limit (sequence)"

From Maths
Jump to: navigation, search
(Created page with ":: '''Note: ''' see Limit page for other kinds of limits __TOC__ ==Definition== Given a sequence {{M|1=(x_n)_{n=1}^\infty\subseteq X}}, a metric space {{M|(X,d)}}...")
 
m (→‎Process)
Line 53: Line 53:
 
If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}}
 
If {{M|x\notin X}} then {{M|d(x_n,x)}} is undefined, as {{M|d:X\times X\rightarrow\mathbb{R}_{\ge_0} }}, that is the [[metric space|distance metric]] is only defined for things in {{M|X}}
 
===Process===
 
===Process===
−
The idea is that defining "tends towards {{M|x}}" is rather difficult, to sidestep this we just say "we can get as close as we like to" instead. This is the purpose of {{M|\epsilon}}.
+
{{Begin Theorem}}
 +
[[Limit (sequence)/Discussion of definition|Discussion of why the definition is what it is.]]
 +
{{Begin Proof}}
 +
{{:Limit (sequence)/Discussion of definition}}
  
−
We say that "if you give me an {{M|\epsilon>0}} - as small as you like - I can find you a point of the sequence ({{M|N}}) where '''''all''''' points after are ''within'' {{M|\epsilon}} of {{M|x}} (where {{M|d(\cdot,\cdot)}} is our notion of distance)
+
{{End Proof}}{{End Theorem}}
−
* That is after {{M|N}} in the sequence, so that's {{M|x_{n+1},x_{n+1},\ldots}} the ''distance'' between {{M|x_{N+i} }} and {{M|x}} is {{M|<\epsilon}}
+
−
*: This is exactly what {{M|n>N\implies d(x_n,x)<\epsilon}} says, it says that:
+
−
*:* whenever {{M|n>N}} we must have {{M|d(x_n,x)<\epsilon}}
+
−
As per the nature of [[implies]] we ''may'' have {{M|d(x_n,x)<\epsilon}} without {{M|n>N}}, it is only important that WHENEVER we are beyond {{M|N}} in the sequence that {{M|d(x_n,x)<\epsilon}}
+
−
{| class="wikitable" border="1"
+
−
|-
+
−
! colspan="2" | Example
+
−
|-
+
−
| [[File:Sequencelimit.gif]]
+
−
| Here:
+
−
* {{M|x}}-axis scale is from {{M|0}} to {{M|12.6}}, marks are shown every unit.
+
−
* {{M|y}}-axis scale starts from {{M|0}} and is marked every {{M|0.25}} units.
+
−
* The sequence is any sequence of points on the wavy function shown.
+
−
** The limit of this is clearly {{M|1}}
+
−
* The two horizontal lines show {{M|1-\epsilon}} and {{M|1+\epsilon}}
+
−
* The vertical line shows one possible value where every point after it is within {{M|\epsilon}} of {{M|1}}
+
−
* '''due to technical limitations the function {{M|1=f(x)=1+\frac{\sin(\pi x)}{\frac{1}{4}x^2} }} is shown'''
+
−
* The curves are bounds on the function.
+
−
|}
+
−
Notice that at {{M|1=x=1}} that {{M|f(1)=1}}, in fact the curve is ''within'' {{M|\pm\epsilon}} several times before we reach the vertical line, this is the significance of the [[implies]] sign, when we write {{M|A\implies B}} we require that ''whenever'' {{M|A}} is true, {{M|B}} must be true, but {{M|B}} may be true regardless of what {{M|A}} is.
+
  
−
Note that ''after'' the vertical line the function is ''always'' within the bounds.
 
−
 
−
Because of this any {{M|N'>N}} may be used too, as if {{M|n>N'}} and {{M|N'>N}} then {{M|n>N'>N}} so {{M|n>N}} - this proves that if {{M|N}} works then any larger {{M|N'}} will too. There is no requirement to find the smallest {{M|N}} that'll work, just ''an'' {{M|N}} such that {{M|n>N\implies d(x_n,x)<\epsilon}}
 
 
==See also==
 
==See also==
 
* [[Cauchy sequence]]
 
* [[Cauchy sequence]]

Revision as of 13:38, 5 December 2015

Note: see Limit page for other kinds of limits

Definition

Given a sequence [ilmath](x_n)_{n=1}^\infty\subseteq X[/ilmath], a metric space [ilmath](X,d)[/ilmath] (that is complete) and a point [ilmath]x\in X[/ilmath], the sequence [ilmath](x_n)[/ilmath] is said to[1][Note 1]:

  • have limit [ilmath]x[/ilmath] or converge to [ilmath]x[/ilmath]

When:

  • [math]\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}[n>N\implies d(x,x_n)<\epsilon][/math][Note 2]
    (note that [ilmath]\epsilon\in\mathbb{R} [/ilmath], obviously - as the co-domain of [ilmath]d[/ilmath] is [ilmath]\mathbb{R} [/ilmath])
  • Read this as:
    for all [ilmath]\epsilon[/ilmath] greater than zero, there exists an [ilmath]N[/ilmath] in the natural numbers such that for all [ilmath]n[/ilmath] that are also natural we have that:
    whenever [ilmath]n[/ilmath] is beyond [ilmath]N[/ilmath] that [ilmath]x_n[/ilmath] is within [ilmath]\epsilon[/ilmath] of [ilmath]x[/ilmath]

Equivalent definitions

Note: where it is not obvious changes have a [ilmath]\{ [/ilmath] underneath them

[math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[\underbrace{n\ge N}\implies d(x_n,x)<\epsilon\right][/math]

Here we have two definitions

  1. [math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[n> N\implies d(x_n,x)<\epsilon\right][/math] (given at the top of the page)
  2. [math]\lim_{n\rightarrow\infty}(x_n)=x\iff\forall\epsilon>0\exists N\in\mathbb{N}\forall n\in\mathbb{N}\left[n\ge N\implies d(x_n,x)<\epsilon\right][/math]

Proof: [ilmath]1\implies 2[/ilmath]

Let [ilmath]\epsilon >0[/ilmath] be given.
We know [ilmath]\exists N'\in\mathbb{N} [/ilmath] such that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath] by assuming [ilmath]1[/ilmath] is true
Choose [ilmath]N=N'+1[/ilmath]
Now [ilmath]n\ge N\implies[n>N\vee n=N][/ilmath] by definition of [ilmath]\ge[/ilmath], substituting [ilmath]N=N'+1[/ilmath] we get [ilmath]n\ge N'+1\implies[n>N'+1\vee n=N'+1][/ilmath]
  • (Case: [ilmath]n>N'+1[/ilmath]) Note that [ilmath]n>N'+1>N'[/ilmath] so by transitivity of [ilmath]>[/ilmath] we see [ilmath]n>N'[/ilmath]
    We know from [ilmath]1[/ilmath] that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath]
  • (Case: [ilmath]n=N'+1[/ilmath]), trivially [ilmath]N'+1>N'[/ilmath] so we have so [ilmath]n>N'[/ilmath]
    We know from [ilmath]1[/ilmath] that [ilmath]n>N'\implies d(x_n,x)<\epsilon[/ilmath]
So in either case we have [ilmath]d(x_n,x)<\epsilon[/ilmath]
  • We have shown that if [ilmath]n\ge N[/ilmath] we have [ilmath]d(x_n,x)\epsilon[/ilmath]
  • Thus choosing [ilmath]N=N'+1[/ilmath] is "an [ilmath]N[/ilmath] that exists" for the given [ilmath]\epsilon[/ilmath]
This completes the first part of the proof

Proof: [ilmath]2\implies 1[/ilmath]

Let [ilmath]\epsilon>0[/ilmath] be given.
We know [ilmath]\exists N'\in\mathbb{N} [/ilmath] such that [ilmath]n\ge N'\implies d(x_n,x)<\epsilon[/ilmath] by assuming [ilmath]2[/ilmath] is true
Choose [ilmath]N=N'-1[/ilmath]
Now [ilmath]n> N\implies n>N'-1[/ilmath]
  • (Case: [ilmath]n=N'[/ilmath]) if this is the case we know that [ilmath]N'>N'-1[/ilmath] so [ilmath]n>N[/ilmath] is satisfied, but also so is [ilmath]n\ge N'[/ilmath] (we have equality)
    We know from [ilmath]2[/ilmath] that this [ilmath]\implies d(x_n,x)<\epsilon[/ilmath]
  • (Case: [ilmath]n>N'[/ilmath]) well [ilmath]n\ge N'[/ilmath] means "if [ilmath]n>N'[/ilmath] or [ilmath]n=N'[/ilmath]" so [ilmath]n>N'\implies n\ge N'[/ilmath], thus [ilmath]n\ge N'[/ilmath]
    We know from [ilmath]2[/ilmath] that this [ilmath]\implies d(x_n,x)<\epsilon[/ilmath]
Thus for [ilmath]n>N[/ilmath] we see that [ilmath]d(x_n,x)<\epsilon[/ilmath]
This completes the proof

(End of proof)

Discussion

Requiring [ilmath]x\in X[/ilmath]

If [ilmath]x\notin X[/ilmath] then [ilmath]d(x_n,x)[/ilmath] is undefined, as [ilmath]d:X\times X\rightarrow\mathbb{R}_{\ge_0} [/ilmath], that is the distance metric is only defined for things in [ilmath]X[/ilmath]

Process

Discussion of why the definition is what it is.

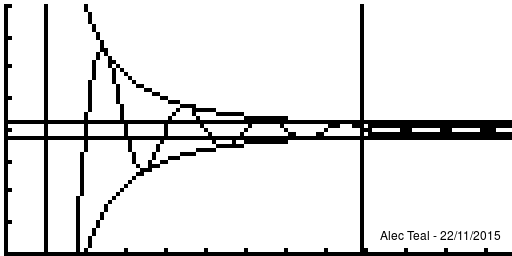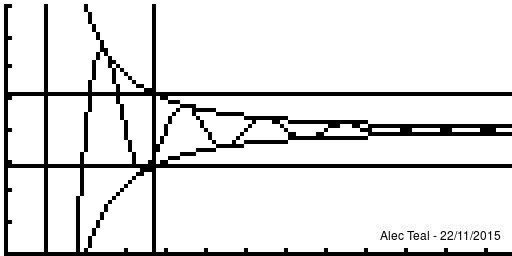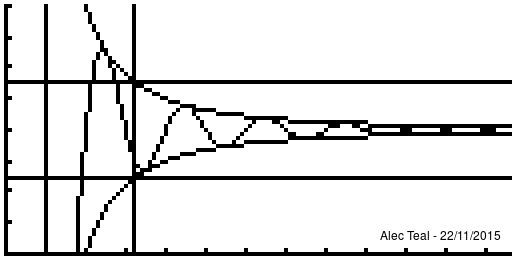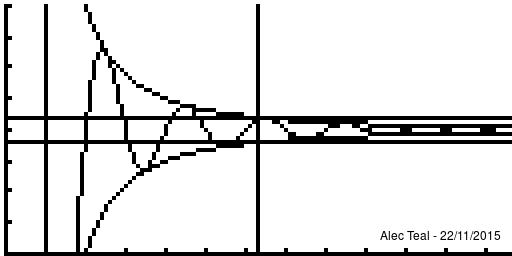
The idea is that defining "tends towards [ilmath]x[/ilmath]" is rather difficult, to sidestep this we just say "we can get as close as we like to" instead. This is the purpose of [ilmath]\epsilon[/ilmath].

We say that "if you give me an [ilmath]\epsilon>0[/ilmath] - as small as you like - I can find you a point of the sequence ([ilmath]N[/ilmath]) where all points after are within [ilmath]\epsilon[/ilmath] of [ilmath]x[/ilmath] (where [ilmath]d(\cdot,\cdot)[/ilmath] is our notion of distance)

  • That is after [ilmath]N[/ilmath] in the sequence, so that's [ilmath]x_{n+1},x_{n+1},\ldots[/ilmath] the distance between [ilmath]x_{N+i} [/ilmath] and [ilmath]x[/ilmath] is [ilmath]<\epsilon[/ilmath]
    This is exactly what [ilmath]n>N\implies d(x_n,x)<\epsilon[/ilmath] says, it says that:
    • whenever [ilmath]n>N[/ilmath] we must have [ilmath]d(x_n,x)<\epsilon[/ilmath]

As per the nature of implies we may have [ilmath]d(x_n,x)<\epsilon[/ilmath] without [ilmath]n>N[/ilmath], it is only important that WHENEVER we are beyond [ilmath]N[/ilmath] in the sequence that [ilmath]d(x_n,x)<\epsilon[/ilmath]

Example
Sequencelimit.gif Here:
  • [ilmath]x[/ilmath]-axis scale is from [ilmath]0[/ilmath] to [ilmath]12.6[/ilmath], marks are shown every unit.
  • [ilmath]y[/ilmath]-axis scale starts from [ilmath]0[/ilmath] and is marked every [ilmath]0.25[/ilmath] units.
  • The sequence is any sequence of points on the wavy function shown.
    • The limit of this is clearly [ilmath]1[/ilmath]
  • The two horizontal lines show [ilmath]1-\epsilon[/ilmath] and [ilmath]1+\epsilon[/ilmath]
  • The vertical line shows one possible value where every point after it is within [ilmath]\epsilon[/ilmath] of [ilmath]1[/ilmath]
  • due to technical limitations the function [ilmath]f(x)=1+\frac{\sin(\pi x)}{\frac{1}{4}x^2}[/ilmath] is shown
  • The curves are bounds on the function.

Notice that at [ilmath]x=1[/ilmath] that , in fact the curve is within [ilmath]\pm\epsilon[/ilmath] several times before we reach the vertical line, this is the significance of the implies sign, when we write [ilmath]A\implies B[/ilmath] we require that whenever [ilmath]A[/ilmath] is true, [ilmath]B[/ilmath] must be true, but [ilmath]B[/ilmath] may be true regardless of what [ilmath]A[/ilmath] is.

Note that after the vertical line the function is always within the bounds.

Because of this any [ilmath]N'>N[/ilmath] may be used too, as if [ilmath]n>N'[/ilmath] and [ilmath]N'>N[/ilmath] then [ilmath]n>N'>N[/ilmath] so [ilmath]n>N[/ilmath] - this proves that if [ilmath]N[/ilmath] works then any larger [ilmath]N'[/ilmath] will too. There is no requirement to find the smallest [ilmath]N[/ilmath] that'll work, just an [ilmath]N[/ilmath] such that [ilmath]n>N\implies d(x_n,x)<\epsilon[/ilmath]


See also

Notes

  1. ↑ Actually Maurin gives:
    • [math]\forall\epsilon>0\exists N\in\mathbb{N}\forall n[n\ge N\implies d(x_n,x)<\epsilon][/math] (the change is the [ilmath]\ge[/ilmath] sign between the [ilmath]n[/ilmath] and [ilmath]N[/ilmath]) but as we shall see this doesn't matter
  2. ↑ In Krzysztof Maurin's notation this can be written as:
    • [math]\bigwedge_{\epsilon>0}\bigvee_{N\in\mathbb{N} }\bigwedge_{n>N}d(x_n,x)<\epsilon[/math]

References

  1. ↑ Krzysztof Maurin - Analysis - Part 1: Elements
Retrieved from "https://www.maths.kisogo.com/index.php?title=Limit_(sequence)&oldid=1447"