File:R2 top group preimage of 1 to -1 epsilon 0.25 steps 0.125.gif

This is an example image for showing that [ilmath](\mathbb{R}-\{0\},\times)[/ilmath] is a topological group. Consider [ilmath]m:(\mathbb{R}-\{0\})\times(\mathbb{R}-\{0\})\rightarrow\mathbb{R}-\{0\} [/ilmath] given by [ilmath]m:(x,y)\mapsto xy[/ilmath], as the example shows [ilmath]m[/ilmath] is continuous (when [ilmath](\mathbb{R}-\{0\})^2 [/ilmath] is considered with the product topology), an important step in doing that is showing that:

• Given an open ball, [ilmath]B_\epsilon(c)[/ilmath] which is, in this case, the open interval [ilmath](c-\epsilon,c+\epsilon)[/ilmath] we must show that the preimage is open (among other things of course).

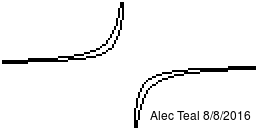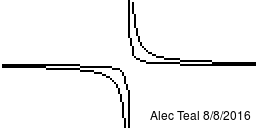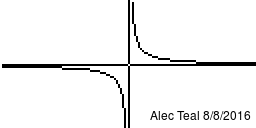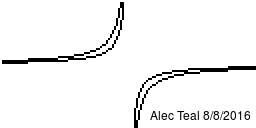
This image shows the preimage of [ilmath](c-\epsilon,c+\epsilon)[/ilmath] as [ilmath]c[/ilmath] goes from [ilmath]-1[/ilmath] to [ilmath]1[/ilmath] in steps of [ilmath]0.125[/ilmath]. For [ilmath]\epsilon:=0.25[/ilmath].

You can see for [ilmath]c=0[/ilmath] the image is symmetric about the [ilmath]x[/ilmath]-axis, [ilmath]y[/ilmath]-axis, [ilmath]y=x[/ilmath] line and [ilmath]y=-x[/ilmath] line and forms like a 4-point star shape. This technically isn't in the space we're dealing with, however we do see the preimage of [ilmath](-0.25,0.25)[/ilmath] in the space.