Limit (sequence)/Discussion of definition

The idea is that defining "tends towards $x$" is rather difficult, to sidestep this we just say "we can get as close as we like to" instead. This is the purpose of $\epsilon$.

We say that "if you give me an $\epsilon>0$ - as small as you like - I can find you a point of the sequence ($N$) where all points after are within $\epsilon$ of $x$ (where $d(\cdot,\cdot)$ is our notion of distance)

• That is after $N$ in the sequence, so that's $x_{n+1},x_{n+1},\ldots$ the distance between $x_{N+i}$ and $x$ is $<\epsilon$

  This is exactly what $n>N\implies d(x_n,x)<\epsilon$ says, it says that:

  • whenever $n>N$ we must have $d(x_n,x)<\epsilon$

As per the nature of implies we may have $d(x_n,x)<\epsilon$ without $n>N$, it is only important that WHENEVER we are beyond $N$ in the sequence that $d(x_n,x)<\epsilon$

Example

Here: $x$-axis scale is from $0$ to $12.6$, marks are shown every unit. $y$-axis scale starts from $0$ and is marked every $0.25$ units. The sequence is any sequence of points on the wavy function shown. The limit of this is clearly $1$ The two horizontal lines show $1-\epsilon$ and $1+\epsilon$ The vertical line shows one possible value where every point after it is within $\epsilon$ of $1$ due to technical limitations the function $f(x)=1+\frac{\sin(\pi x)}{\frac{1}{4}x^2}$ is shown The curves are bounds on the function.

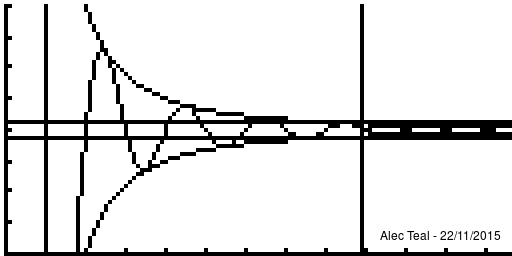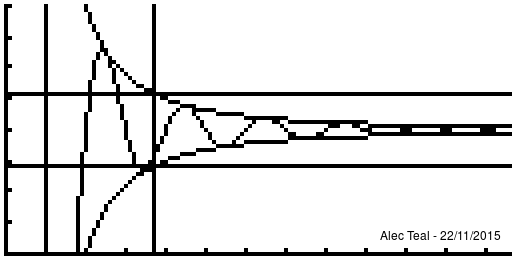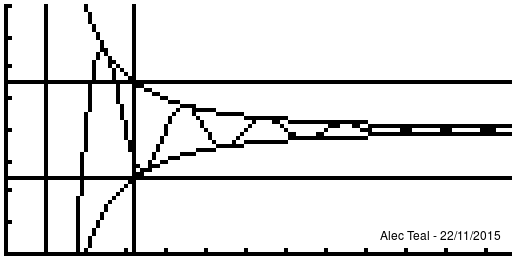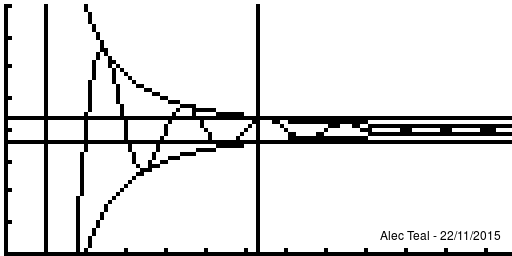
Notice that at $x=1$ that , in fact the curve is within $\pm\epsilon$ several times before we reach the vertical line, this is the significance of the implies sign, when we write $A\implies B$ we require that whenever $A$ is true, $B$ must be true, but $B$ may be true regardless of what $A$ is.

Note that after the vertical line the function is always within the bounds.

Because of this any $N'>N$ may be used too, as if $n>N'$ and $N'>N$ then $n>N'>N$ so $n>N$ - this proves that if $N$ works then any larger $N'$ will too. There is no requirement to find the smallest $N$ that'll work, just an $N$ such that $n>N\implies d(x_n,x)<\epsilon$